Simple calculator

_{This page (including the images) was contributed by ynn.}

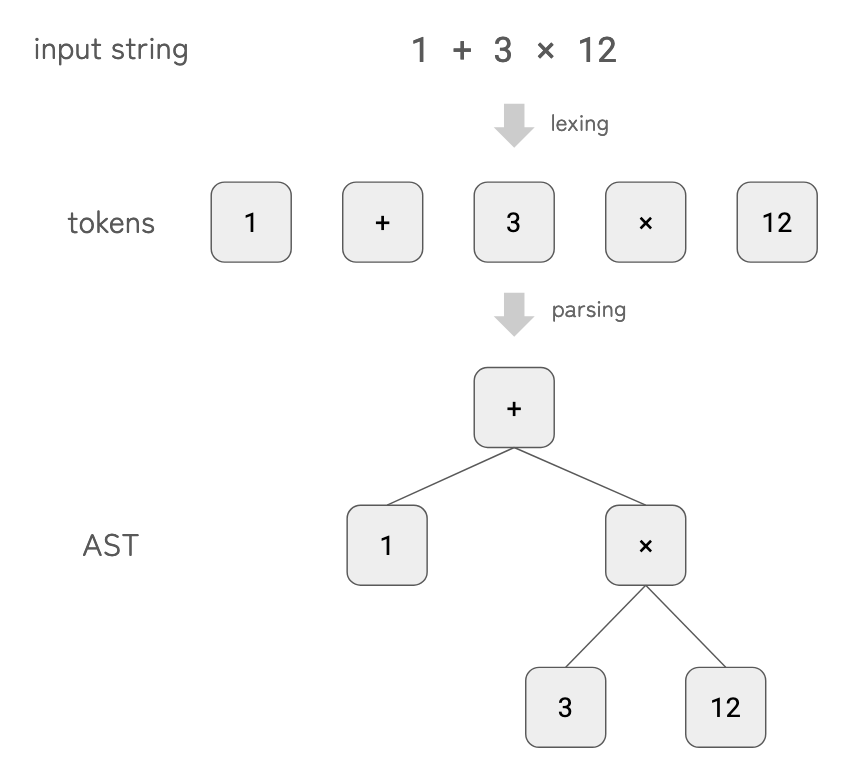
When you implement an interpreter for a domain-specific language (DSL), or any programming language, the process typically involves the following steps:

Lexing: Splitting the input stream (i.e., source code string) into tokens via a lexer.
Parsing: Converting the tokens into an abstract syntax tree (AST) via a parser.
Evaluation: Evaluating the AST to produce the result.

In this example, we implement a simple calculator that evaluates arithmetic expressions such as 1 + 2 * 3 or ((1 + 2) * 3 + 4) * 2 + 4 / 3.

We use logos as the lexer generator and chumsky as the parser library.

flow chart

1. Try It

Before diving into the implementation details, let’s play with it¹.

$ cargo run --example calculator '1 + 7 * (3 - 4) / 2'

Output:

[AST]
Add(
    Int(
        1,
    ),
    Div(
        Mul(
            Int(
                7,
            ),
            Sub(
                Int(
                    3,
                ),
                Int(
                    4,
                ),
            ),
        ),
        Int(
            2,
        ),
    ),
)

[result]
-2

Full source code

use std::env;

use chumsky::prelude::*;
use logos::Logos;

#[derive(Logos, Debug, PartialEq, Eq, Hash, Clone)]
#[logos(skip r"[ \t\n]+")]
#[logos(error = String)]
enum Token {
    #[token("+")]
    Plus,

    #[token("-")]
    Minus,

    #[token("*")]
    Multiply,

    #[token("/")]
    Divide,

    #[token("(")]
    LParen,

    #[token(")")]
    RParen,

    #[regex("[0-9]+", |lex| lex.slice().parse::<isize>().unwrap())]
    Integer(isize),
}

#[derive(Debug)]
enum Expr {
    // Integer literal.
    Int(isize),

    // Unary minus.
    Neg(Box<Expr>),

    // Binary operators.
    Add(Box<Expr>, Box<Expr>),
    Sub(Box<Expr>, Box<Expr>),
    Mul(Box<Expr>, Box<Expr>),
    Div(Box<Expr>, Box<Expr>),
}

impl Expr {
    fn eval(&self) -> isize {
        match self {
            Expr::Int(n) => *n,
            Expr::Neg(rhs) => -rhs.eval(),
            Expr::Add(lhs, rhs) => lhs.eval() + rhs.eval(),
            Expr::Sub(lhs, rhs) => lhs.eval() - rhs.eval(),
            Expr::Mul(lhs, rhs) => lhs.eval() * rhs.eval(),
            Expr::Div(lhs, rhs) => lhs.eval() / rhs.eval(),
        }
    }
}

#[allow(clippy::let_and_return)]
fn parser<'src>(
) -> impl Parser<'src, &'src [Token], Expr, chumsky::extra::Err<chumsky::error::Simple<'src, Token>>>
{
    recursive(|p| {
        let atom = {
            let parenthesized = p
                .clone()
                .delimited_by(just(Token::LParen), just(Token::RParen));

            let integer = select! {
                Token::Integer(n) => Expr::Int(n),
            };

            parenthesized.or(integer)
        };

        let unary = just(Token::Minus)
            .repeated()
            .foldr(atom, |_op, rhs| Expr::Neg(Box::new(rhs)));

        let binary_1 = unary.clone().foldl(
            just(Token::Multiply)
                .or(just(Token::Divide))
                .then(unary)
                .repeated(),
            |lhs, (op, rhs)| match op {
                Token::Multiply => Expr::Mul(Box::new(lhs), Box::new(rhs)),
                Token::Divide => Expr::Div(Box::new(lhs), Box::new(rhs)),
                _ => unreachable!(),
            },
        );

        let binary_2 = binary_1.clone().foldl(
            just(Token::Plus)
                .or(just(Token::Minus))
                .then(binary_1)
                .repeated(),
            |lhs, (op, rhs)| match op {
                Token::Plus => Expr::Add(Box::new(lhs), Box::new(rhs)),
                Token::Minus => Expr::Sub(Box::new(lhs), Box::new(rhs)),
                _ => unreachable!(),
            },
        );

        binary_2
    })
}

fn main() {
    //reads the input expression from the command line
    let input = env::args()
        .nth(1)
        .expect("Expected expression argument (e.g. `1 + 7 * (3 - 4) / 5`)");

    //creates a lexer instance from the input
    let lexer = Token::lexer(&input);

    //splits the input into tokens, using the lexer
    let mut tokens = vec![];
    for (token, span) in lexer.spanned() {
        match token {
            Ok(token) => tokens.push(token),
            Err(e) => {
                println!("lexer error at {:?}: {}", span, e);
                return;
            }
        }
    }

    //parses the tokens to construct an AST
    let ast = match parser().parse(&tokens).into_result() {
        Ok(expr) => {
            println!("[AST]\n{:#?}", expr);
            expr
        }
        Err(e) => {
            println!("parse error: {:#?}", e);
            return;
        }
    };

    //evaluates the AST to get the result
    println!("\n[result]\n{}", ast.eval());
}

2. Lexer

Our calculator supports the following tokens:

Integer literals: 0, 1, 15, etc;
Unary operator: -;
Binary operators: +, -, *, /;
Parenthesized expressions: (3 + 5) * 2, ((1 + 2) * 3 + 4) * 2 + 3 / 2, etc.

#[derive(Logos, Debug, PartialEq, Eq, Hash, Clone)]
#[logos(skip r"[ \t\n]+")]
#[logos(error = String)]
enum Token {
    #[token("+")]
    Plus,

    #[token("-")]
    Minus,

    #[token("*")]
    Multiply,

    #[token("/")]
    Divide,

    #[token("(")]
    LParen,

    #[token(")")]
    RParen,

    #[regex("[0-9]+", |lex| lex.slice().parse::<isize>().unwrap())]
    Integer(isize),
}

3. Parser

While it is easy enough to manually implement a parser in this case (e.g., Pratt parsing), let’s just use the chumsky crate, which is a popular parser combinator library in Rust.

3.1 AST Definition

First, we define the AST.

#[derive(Debug)]
enum Expr {
    // Integer literal.
    Int(isize),

    // Unary minus.
    Neg(Box<Expr>),

    // Binary operators.
    Add(Box<Expr>, Box<Expr>),
    Sub(Box<Expr>, Box<Expr>),
    Mul(Box<Expr>, Box<Expr>),
    Div(Box<Expr>, Box<Expr>),
}

Note that

We name the enum not AST but Expr because an AST is just nested expressions.
There is no Parenthesized variant because parentheses only affect the order of operations (i.e., precedence), which is reflected in the AST structure.
Box is used as a recursive enum is not allowed in Rust.

Next, we define the parser. The code may look a bit complicated if you are not familiar with parser combinator libraries, but it is actually quite simple. See Chumsky’s official tutorial for the details.

fn parser<'src>(
) -> impl Parser<'src, &'src [Token], Expr, chumsky::extra::Err<chumsky::error::Simple<'src, Token>>>
{
    recursive(|p| {
        let atom = {
            let parenthesized = p
                .clone()
                .delimited_by(just(Token::LParen), just(Token::RParen));

            let integer = select! {
                Token::Integer(n) => Expr::Int(n),
            };

            parenthesized.or(integer)
        };

        let unary = just(Token::Minus)
            .repeated()
            .foldr(atom, |_op, rhs| Expr::Neg(Box::new(rhs)));

        let binary_1 = unary.clone().foldl(
            just(Token::Multiply)
                .or(just(Token::Divide))
                .then(unary)
                .repeated(),
            |lhs, (op, rhs)| match op {
                Token::Multiply => Expr::Mul(Box::new(lhs), Box::new(rhs)),
                Token::Divide => Expr::Div(Box::new(lhs), Box::new(rhs)),
                _ => unreachable!(),
            },
        );

        let binary_2 = binary_1.clone().foldl(
            just(Token::Plus)
                .or(just(Token::Minus))
                .then(binary_1)
                .repeated(),
            |lhs, (op, rhs)| match op {
                Token::Plus => Expr::Add(Box::new(lhs), Box::new(rhs)),
                Token::Minus => Expr::Sub(Box::new(lhs), Box::new(rhs)),
                _ => unreachable!(),
            },
        );

        binary_2
    })
}

4. Evaluator

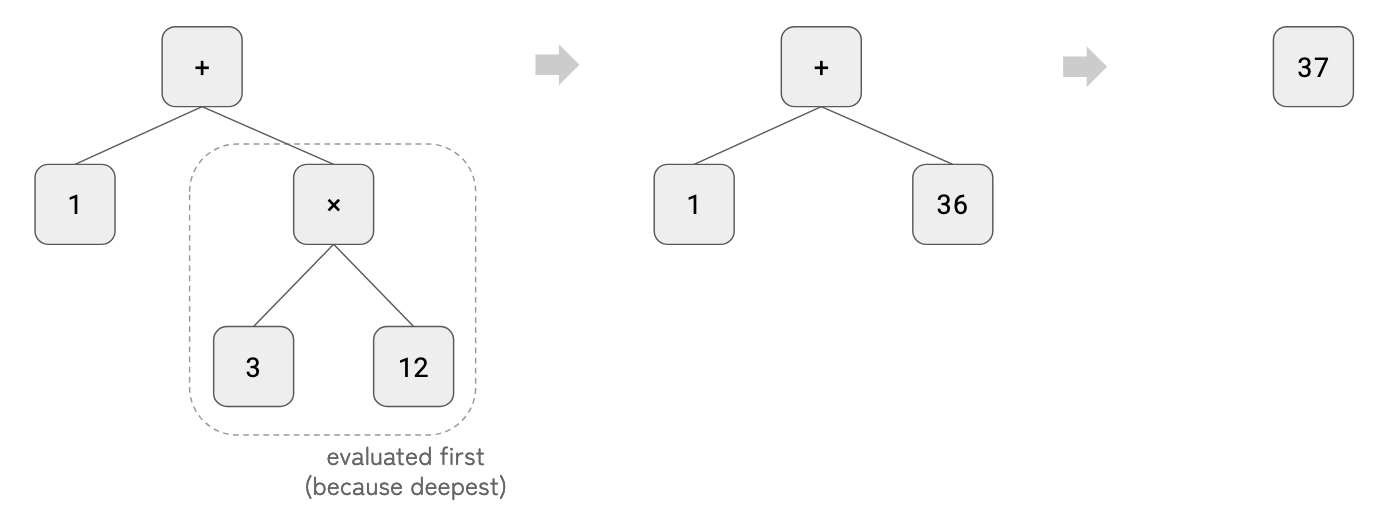
Evaluating the AST is straightforward. We just implement it using depth-first search (DFS) such that the mathematical operations are processed in the correct order.

impl Expr {
    fn eval(&self) -> isize {
        match self {
            Expr::Int(n) => *n,
            Expr::Neg(rhs) => -rhs.eval(),
            Expr::Add(lhs, rhs) => lhs.eval() + rhs.eval(),
            Expr::Sub(lhs, rhs) => lhs.eval() - rhs.eval(),
            Expr::Mul(lhs, rhs) => lhs.eval() * rhs.eval(),
            Expr::Div(lhs, rhs) => lhs.eval() / rhs.eval(),
        }
    }
}

Example

Evaluating 1 + 3 * 12 will proceed as below.

how evaluator works

5. `main()` Function

Finally, we put everything together in the main() function.

fn main() {
    //reads the input expression from the command line
    let input = env::args()
        .nth(1)
        .expect("Expected expression argument (e.g. `1 + 7 * (3 - 4) / 5`)");

    //creates a lexer instance from the input
    let lexer = Token::lexer(&input);

    //splits the input into tokens, using the lexer
    let mut tokens = vec![];
    for (token, span) in lexer.spanned() {
        match token {
            Ok(token) => tokens.push(token),
            Err(e) => {
                println!("lexer error at {:?}: {}", span, e);
                return;
            }
        }
    }

    //parses the tokens to construct an AST
    let ast = match parser().parse(&tokens).into_result() {
        Ok(expr) => {
            println!("[AST]\n{:#?}", expr);
            expr
        }
        Err(e) => {
            println!("parse error: {:#?}", e);
            return;
        }
    };

    //evaluates the AST to get the result
    println!("\n[result]\n{}", ast.eval());
}

6. Extend the Calculator

Now that you’ve implemented a basic calculator, try extending its functionality with the following tasks:

Handle zero-division gracefully: The current evaluator panics when zero-division occurs. Change the return type of the evaluator from isize to Result<isize, String>, making it possible to return an error message.
Add support for the modulo operator (%): Update the lexer, parser, and evaluator to handle expressions like 10 % 3.
Add support for built-in functions: Implement built-in functions such as abs(x), pow(x, y) or rand().

You first need to clone this repository. ↩

Logos Handbook